Pierwsza zasada termodynamiki
UWAGA: prezentowany tekst jest fragmentem rozdziału drugiego tomu podręcznika do nauki obliczeń chemicznych, którego premierę przewidujemy na przełomie listopada i grudnia.
Entalpia przemiany i podział procesów ze względu na kierunek wymiany energii.
Wiemy już, że krzepnięciu wody towarzyszy wydzielenie ciepła do otoczenia. Ale! Zamrażając zupy czy sosy w słoikach i innych szklanych naczyniach trzeba uważać. Dlaczego? Nieraz dzieci mają za zadanie wykonać doświadczenie, podczas którego należy zostawić na mrozie słoik wypełniony zimną wodą. Następnego dnia okazuje się, że w słoiku, owszem, jest lód, ale oprócz tego słoik popękał. Wynika z tego, że wydzielenie ciepła to nie jest jedyne zjawisko, które towarzyszy zamarzaniu wody. Zostaje rozerwany słoik, czyli jest także wykonana jakaś praca przez układ. Zatem przemianie towarzyszą w rzeczywistości zarówno wymiana ciepła, jak i dodatkowo wykonanie pracy. Ten przykład posłużył temu, by nas wprowadzić do tzw. pierwszej zasady termodynamiki, której treść poznamy już teraz:
Zmiana energii wewnętrznej układu zamkniętego jest równa sumie wymienionego z otoczeniem ciepła oraz pracy wykonanej przez układ na otoczeniu, lub przez otoczenie na układzie.
Co zapisujemy prostym wzorem:
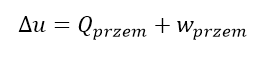
Lub możemy też możemy zapisać inaczej:

Gdzie ΔEciepło oznacza ilość energii wymienionej z otoczeniem na sposób ciepła, a ΔEpraca to ilość energii wymienionej z otoczeniem na sposób pracy. Obydwa równania oznaczają dokładnie to samo.
Wykonanie pracy to nie tylko ruch, to także zmiana kształtu, jak jest w naszym przypadku. Przez zmianę kształtu rozumiemy także zmianę objętości. Lód ma niższą gęstość niż ciekła woda, toteż ta sama masa lodu zajmuje większą objętość niż ciecz. To sprawia, że lód unosi się na wodzie, a rosnąca objętość sprawia, że zostaje rozerwany słoik czy też uwięziona w szczelinie woda zamarzając rozrywa twarde skały albo beton. Albo powoduje powstawanie dziur w drogach.
Przypomnijmy sobie doświadczenie z pierwszego tomu z zamkniętą palcem strzykawką i zachowaniem tłoka podczas naciskania tłoka, a potem jego zwalniania. Naciskanie tłoka powoduje sprężanie gazu – zmniejszenie jego objętości, a zwolnienie tłoka powoduje jego rozprężenie – zwiększenie objętości. Dociskając tłok – wykonaliśmy pracę na układzie, którym był gaz w strzykawce. Zwalniając tłok, to gaz wykonuje pracę na otoczeniu i tłok się cofa. Co się stało z energią? Najpierw sprężając gaz przekazaliśmy energię do układu, czyli do gazu. My, jako otoczenie, wykonaliśmy pracę na układzie. W momencie zwolnienia tłoka to gaz przekazał część własnej energii (czyli energii wewnętrznej) do otoczenia wykonując pracę na otoczeniu – zwiększając objętość. Zatem sprężony gaz miał wyższą energię wewnętrzną, niż rozprężony. Pracę związaną ze zmianą objętości układu nazywamy pracą objętościową. Definiowana jest następująco:

Jest ona iloczynem zmiany objętości oraz ciśnienia, a ciśnienie jest siłą wykonującą tę pracę. Jeśli podczas przemiany objętość układu rośnie, to układ wykonuje pracę na otoczeniu przeciwko ciśnieniu zewnętrznemu – tak jak przy zamarzaniu wody. Z kolei jeśli podczas przemiany objętość spada, to ciśnienie zewnętrzne wykonuje pracę na układzie. I tak ciśnienie wytwarzane przez lód rozrywa słoik podczas zamarzania (układ wykonuje pracę na otoczeniu), zaś ciśnienie zewnętrzne odpowiada za skurcz objętości podczas topnienia lodu. Tak jak ciepło, tak i praca ma znak informujący nas o tym, w którą stronę wykonywana jest praca. Jeśli układ zwiększa swoją objętość, to wykonuje pracę na otoczeniu: taka praca otrzymuje znak ujemny, bo układ traci własną energię na wykonanie pracy. Jeśli układ zmniejsza swoją objętość, to otoczenie wykonuje pracę na układzie – układ na sposób pracy zyskuje energię.

Funkcją, która wiąże ze sobą energię wewnętrzną układu oraz jego zdolność do wykonania pracy objętościowej jest entalpia. Entalpię danego ciała określa wzór:

lub w przypadku 1 mola substancji:

Iloczyn pV jest pracą wykonaną przez dany układ (ciało), by zająć jakąś objętość w przestrzeni, zakładając, że zaczynamy od zerowej objętości. Wtedy zmiana objętości jest równa objętości układu:
![]()
Stąd też w ogólnym wzorze na entalpię ciała nie pojawia się zmiana objętości, tylko sama objętość ciała. Entalpię zwiemy inaczej zawartością ciepła, a o tym dlaczego – wkrótce się przekonamy. Trudno jest określić rzeczywistą entalpię danego ciała, a i zazwyczaj nie jest nam to potrzebne, gdyż najczęściej skupiamy się na entalpii przemiany, czyli zmianie entalpii układu, która ma miejsce podczas przemiany zachodzącej w tym układzie. Dokładny sens tej funkcji termodynamicznej zostanie podany po rozpatrzeniu trzech przypadków poniżej, gdzie zostanie też dokładnie wyprowadzony wzór, a na tę chwilę zapamiętajmy jedynie ogólną definicję entalpii przemiany:

A posługując się wielkościami molowymi:

Rozpatrzymy teraz razem trzy przypadki, które pozwolą nam poznać nową funkcję bliżej. Najpierw przypadek reakcji chemicznej syntezy chlorowodoru z pierwiastków.

Zauważmy, że jedna objętość wodoru reaguje z jedną objętością chloru – razem po stronie substratów mamy 2 objętości gazów. Po stronie produktów także mamy dwie objętości gazów – objętość układu nie ulega zmianie podczas przemiany (ΔV=0), czyli nie jest wykonywana praca objętościowa. W tym przypadku układ wymienia energię z otoczeniem jedynie na sposób ciepła, a entalpia przemiany jest równa zmianie energii wewnętrznej układu.
![]()
Zatem w przypadku, gdy praca objętościowa nie jest wykonywana to zmiana energii wewnętrznej odpowiada entalpii przemiany. Jednakże znamy wiele innych przemian, w których następuje wzrost objętości, np. w reakcji rozkładu trójtlenku siarki:

Jeśli w układzie utrzymywane jest stałe ciśnienie, to jeśli przereagują dwie objętości substratu, to otrzymamy 3 objętości produktów. Spróbujmy obliczyć tę pracę, zakładając, że reakcji ulegają dwa mole SO3 i że reakcja ta biegnie w stanie standardowym (1000 hPa, 298,15 K), w których objętość molowa gazów wynosi 24,79 dm3, co musimy zamienić na m3 (jednostkę SI).
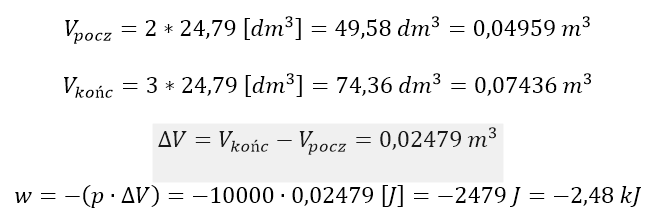
Entalpia tej reakcji w stanie standardowym wynosi 197,78 kJ. Tyle energii z zewnątrz należy dostarczyć do układu i o tyle wzrosłaby jego energia wewnętrzna, gdyby równocześnie układ nie wykonał pracy na otoczeniu ( równej 2,48 kJ), czyli nie stracił części tej energii (stąd znak ujemny). Zauważmy, że w ogólnym rozrachunku układ stracił 1,27% dostarczonej na sposób ciepła energii. Zostało ono zużyte na wykonanie pracy objętościowej, a o pozostałą część dostarczonej energii (195,27 kJ) bogatszy jest teraz nasz układ. Dostarczyliśmy do układu więcej ciepła, niż wzrosła energia układu.
Kolejny przykład będzie dotyczył zmniejszenia objętości. Rozpatrzymy reakcję biegnącą w fazie gazowej:

Reakcji tej towarzyszy spadek objętości o połowę, bo z czterech objętości po zakończeniu reakcji pozostają dwie. W tym przypadku to otoczenie wykonuje pracę na układzie – ciśnienie zewnętrzne powoduje ściśnięcie go do mniejszej objętości. Układ zyskuje dzięki temu dodatkową porcję energii. Jaką konkretnie? Zakładając, że reakcja przebiega w stanie standardowym – przemianie trzech moli wodoru i jednego mola azotu towarzyszy spadek objętości o 49,57 dm3 (ΔV<0), co odpowiada pracy:
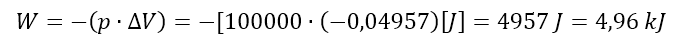
Entalpia tej reakcji wynosi -91,88 kJ (przy założeniu, że reagują 3 mole wodoru z molem azotu), czyli układ oddaje energię poprzez wymianę ciepła, ale jednocześnie przyjmuje energię od otoczenia na sposób pracy.
Zauważyliśmy zaiste znak ujemny we wzorze na pracę objętościową, którego najpierw nie podałem w definicji. Nie ma pracy ujemnej. Znak ten wynika z przyjętej konwencji – rozpatrujemy energię układu, która rośnie, gdy otoczenie zmniejsza jego objętość. Wtedy zmiana objętości jest ujemna i praca też miałaby znak ujemny. Dodatkowy minus we wzorze daje znak dodatni – w końcu układ zyskuje energię. Z kolei gdy układ traci energię na zwiększenie swojej objętości – praca objętościowa wyszłaby dodatnia, ale minus pozwala uwzględnić, że układ musiał wykorzystać część własnej energii na jej wykonanie i jest w nią uboższy.
Wróćmy do zamarzania wody (patrz: przykład 4). Jaka praca zostanie wykonania podczas zamarzania 500 g wody? W temperaturze 0 lód ma gęstość 0,9167 g/ml, a woda ciekła 0,9998 g/ml. Obliczymy przyrost objętości:

Jednakże tę wartość musimy przeliczyć na m3 (SI), otrzymując 0,0000453 m3. Policzmy teraz jaką pracę wykonał układ podczas zamarzania:
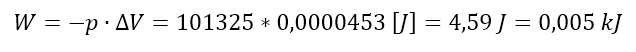
Chociaż słoik zostaje rozerwany, to jest to niewielka praca ze względu na niewielki przyrost objętości. Z przykładu 4. otrzymaliśmy, że podczas zamarzania 500 g wody wydziela się 166,850 kJ ciepła. Jeśli dodamy do tego pracę objętościową, to po korekcie otrzymamy, że układ pozbył się 166,855 kJ energii. Liczby te są praktycznie równe.
Aby podsumować rozpatrzmy jeszcze proces odparowania 1 mola (18 g) wody w temperaturze 100 ℃ i pod ciśnieniem otoczenia 1013,25 hPa.

Objętość molowa gazów w tych warunkach wynosi 30,619 dm3. Z kolei objętość molowa ciekłej wody w tej temperaturze – zaledwie ok. 19 ml, czyli 0,019 dm3. Policzmy zmianę objętości:
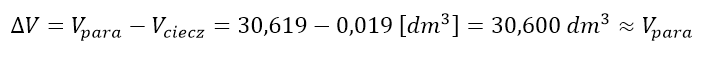
Czyli w przypadku przemian, w których pojawia się lub zanika faza gazowa (gaz lub para substancji), zmiana objętości jest praktycznie równa objętości tej fazy. Praca objętościowa zatem praktycznie nie zależy od objętości fazy ciekłej lub stałej, a od objętości fazy gazowej przed i po zakończeniu przemiany – możemy się przekonać, że podstawiając 30,600 i 30,619 do wzoru na pracę otrzymamy niemal ten sam wynik.
Doszliśmy do momentu w którym wszystko podsumujemy – efekt energetyczny zmiana energii wewnętrznej układu na sposób pracy i ciepła, przy czym jest on równy ciepłu wymienionemu podczas przemiany, gdy nie jest wykonywana praca objętościowa, ani żadna inna praca:

Umownie przyjmujemy, że równość ta jest zachowana, gdy praca objętościowa jest zaniedbywalnie mała (np. podczas topnienia lodu) – nie biorą w niej udziału reagenty gazowe, lub ich liczba nie ulega zmianie podczas przemiany czy to chemicznej, czy to fizycznej. W przypadku gdy objętość układu ulega zdecydowanej zmianie, tj. pojawia się lub zanika reagent gazowy, lub też ulega zmianie liczba cząsteczek/atomów substancji gazowych, to praca objętościowa wpływa w zauważalnym stopniu na efekt energetyczny procesu i ciepło przemiany uwzględnia ten fakt:

Przypomnijmy pierwszą zasadę termodynamiki:
Zmiana energii wewnętrznej układu zamkniętego jest równa sumie wymienionego z otoczeniem ciepła oraz pracy wykonanej przez układ na otoczeniu, lub przez otoczenie na układzie.
Co zapisujemy:

Jeśli przekształcimy ten wzór odejmując pracę od energii wewnętrznej, to otrzymamy:
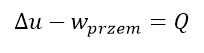
A nasz układ podczas przemiany wykonuje jedynie pracę objętościową:

To otrzymujemy wzór na entalpię przemiany:

Entalpia przemiany jest ciepłem wymienionym przez układ z otoczeniem podczas przemiany, gdy jedyna praca, jaką wykonuje układ, to praca związana ze zmianą własnej objętości przez układ (czyli układ nie może zasilać maszyny itd.). W sytuacji, gdy praca objętościowa wynosi zero (a ściślej: jest pomijalnie mała), to przyjmuje się, że entalpia przemiany jest równa zmianie energii wewnętrznej układu podczas przemiany.

Dlatego też np. podczas zamarzania wody jedyny efekt energetyczny to wymiana ciepła, gdyż udział pracy objętościowej jest zbyt mały, by wpłynął na wynik obliczeń przy założonych zaokrągleniach do 4 cyfr znaczących. Zwróćmy uwagę, jak duża jest różnica pomiędzy energią cieplną, a mechaniczną.
Procesy, w których zmiana entalpii jest ujemna nazywamy egzoenergetycznymi, a procesy w których zmiana ta jest dodatnia zwiemy endoenergetycznymi. W pierwszym przypadku układ ma niższą energię wewnętrzną po przemianie, a w drugim – wyższą. Zauważmy jednak, że układ może zyskiwać energię z zewnątrz poprzez ciepło, ale także równocześnie zwiększać objętość, czyli zużywać własną energię wykonując pracę na otoczeniu, jak w rozpatrywanym przypadku rozkładu SO3. Procesy, w których układ przyjmuje ciepło z otoczenia zwiemy endotermicznymi. W odwrotnym przypadku układ traci ciepło, ale równocześnie zyskuje energię na sposób pracy wykonanej na nim przez otoczenie, takie procesy, w których układ oddaje ciepło, zwiemy egzotermicznymi. Zazwyczaj procesy, egzoenergetyczne są równocześnie egzotermiczne, a endoenergetyczne ze względu na dominujący efekt cieplny nad objętościowym równocześnie endotermiczne. Może się jednak zdarzyć, że efekt cieplny będzie mniejszy niż praca objętościowa i wtedy to praca określa, czy układ zyskuje, czy też traci energię podczas przemiany. W niektórych przemianach mówimy o procesie egzoenergetycznym, który równocześnie jest endotermiczny jak i druga możliwość to proces endoenergetyczny, który równocześnie jest egzotermiczny. Entalpia przemiany określa jej bilans energetyczny. Wyjaśniła się też chyba jej polska nazwa – zawartość ciepła. Jest to po prostu ilość ciepła, którą można odebrać układowi uwzględniając, że podczas odbierania ciepła układ może tracić część energii na wykonanie pracy (wtedy ciepła odbierzemy mniej) lub zyskiwać dodatkową porcję od otoczenia (wtedy ciepła możemy odebrać więcej, niż wynika z początkowej energii wewnętrznej układu). Entalpia przemiany z kolei jest zmianą zawartości ciepła w układzie podczas przemiany.
Pozorna sprzeczność efektu temperaturowego i cieplnego. Zasada zachowania energii.
Jedno z ciekawszych pytań zadawanych przez ludzi podczas nauki o efektach energetycznych, to dlaczego, skoro układ oddaje energię, to dlaczego w reakcji egzotermicznej temperatura układu wzrasta? A dlaczego w procesie endotermicznym temperatura układu maleje, skoro układ zyskuje ciepło? Przecież temperatura wzrasta, gdy dostarczamy ciepła, a maleje, gdy odbieramy ciepło. Np. kaloryfer oddaje ciepło do otoczenia i obniża swoją temperaturę. Jak jednak wyjaśnić, że w procesie oddawania ciepła temperatura wzrasta? Czasem spotykam się z różnym dziwnym uzasadnieniem, łącznie z tym, że uczą tak, a jest odwrotnie, że to są rzeczy, które się filozofom nie śniły itp. Nie jest, i w tym przypadku jest dokładnie tak jak uczą, a sprzeczność jest całkowicie pozorna. Wiemy już, że ta sama masa różnych substancji, ma tę samą energię wewnętrzną w różnych temperaturach, lub też w tej samej temperaturze mają różną energię wewnętrzną. Jeśli zamiast masy będziemy rozpatrywać liczność substancji, to będzie dokładnie tak samo: w temperaturze 20 ℃ 1 kg ciekłej wody ma inną energię niż 1 kg chlorku sodu (soli kuchennej), a 1 mol ciekłej wody ma inną energię wewnętrzną niż 1 mol stałego chlorku sodu. Substancje mają też różną pojemność cieplną – ta sama dawka ciepła spowoduję różną reakcję termiczną soli, jak i wody. A teraz wyobraźmy sobie, że zapukał do naszych drzwi czarodziej. Ale nie jakiś siwobrody starzec w stożkowatym kapeluszu, tylko jakiś młody, niedoświadczony (może to być Harry Potter). Aby udowodnić, że jest czarodziejem, postanowił zamienić 1 kg zimnej wody w sól kuchenną. Masa nie może zniknąć – 1 kg wody zamieni się w 1 kg soli. W tym celu wziął szklany dzbanek do parzenia herbaty, napełnił go 1 kg wody, złapał go w obie dłonie i rzucił zaklęcie. Dzbanek zamiast wody zawiera teraz 1 kg soli – lecz to nie wszystko! Przecież nasz układ ma tę samą energię wewnętrzną – energia w trakcie przemiany nie mogła zniknąć – czary nie mogły spowodować, że energia zniknęła lub się pojawiła. Układ ma więc tę samą energię wewnętrzną, ale inną pojemność cieplną – temperatura soli w dzbanku jest więc inna…. Są więc dwie możliwości – albo dłonie naszego czarodzieja zostaną poparzone, albo zamrożone. Woda znana jest ze swojej bardzo dużej pojemności cieplnej, dlatego nawet bez sprawdzania w tablicach możemy założyć, że sól ma znacznie niższą pojemność cieplną – przy tej samej energii wewnętrznej ma wyższą temperaturę. Dłonie naszego czarodzieja zostaną więc prawdopodobnie poparzone. Nasz czarodziej dobrze nauczył się magii, ale zaniedbał naukę termodynamiki. Nauczony przykrym doświadczeniem – następnym razem wykona tę magiczną sztuczkę w termosie. Ale co się dzieje z solą w dzbanku? Mamy dzbanek z 1 kg gorącej soli. W pokoju jest ok. 20 ℃ – sól zaczyna stygnąć. Sól oddaje ciepło i obniża swoją temperaturę – obniża swoją energię wewnętrzną. Sól będzie oddawać ciepło aż do momentu, gdy temperatury otoczenia i soli ulegną wyrównaniu, czyli układ będzie w równowadze termicznej z otoczeniem. Ostatecznie produkt ma tę samą temperaturę, co substrat przed przemianą, ale niższą energię.
Zwróćmy uwagę, jak oszukują nas autorzy baśni i bajek, a także twórcy filmowi – gdyby konsultowali się czarodziejem, wiedzieliby, że zimną wodę można zamienić w rozżarzone żelazo, stopioną cynę – w lód, a pewnych sztuczek wykonać nie można, bo finalne ciało miałoby temperaturę poniżej zera bezwzględnego – a to niemożliwe, więc nie ma na to zaklęcia. Inne byłyby tak gorące, że przekraczało to by granice ich termicznej stabilności – mogłyby się rozłożyć, więc efekt byłby opłakany. W miarę bezpiecznie można zamienić księżniczkę w żabę, ale za to – bardzo wielką, bo masa nie znika.
Co dzieje się w reakcjach chemicznych? Jedne substancje przechodzą w inne, o innej pojemności cieplnej. Pozwala to nam uogólnić: w przemianach egzotermicznych maleje pojemność cieplna układu, stąd temperatura produktów jest wyższa od początkowej temperatury substratów, a podniesienie temperatury umożliwia oddanie części ciepła do otoczenia (obniżenia energii układu). Z kolei w przemianach endotermicznych – powstają produkty, których pojemność cieplna jest wyższa od pojemności cieplnej substratów – przy tej samej energii wewnętrznej produkty mają niższą temperaturę. Oznacza to, że nastąpi przekazywanie ciepła z otoczenia, do chłodniejszego układu. Energia układu więc wzrasta. Wszystko to wynika z zasady zachowania energii.
Zapamiętaj!
